
Annuitás – mit jelent, és hogyan működik a pénzügyekben?
Mi az a pénzügyi annuitás, és hogyan működik hitelek, befektetések, nyugdíj-megtakarítások esetén? Tudd meg, melyek az annuitás előnyei és hátrányai!
Mi az annuitás?
Az annuitás jelentése az, hogy egy adott időszak során azonos összegű kifizetés történik.
Az annuitás kifejezéssel a legtöbben a hiteltörlesztésüknél találkozhatnak, amikor havonta azonos összegű részletekben fizetnek a banknak. Ez az annuitásos törlesztés.
Emellett azonban az annuitás nyugdíjbiztosítás, életjáradékok, befektetések esetén is megjelenik.
Annuitás a hitelekben
A lakossági ügyfelek számára ma már csak annuitásos hitel érhető el a bankoknál. Ez azért van, hogy kiszámíthatóbb és egyszerűbb legyen a törlesztés: a részletek a kamatperióduson belül ugyanis változatlanok. Ez az annuitás legfőbb előnye. Van azonban hátránya is.
Az annuitás hátránya a törlesztésnél
Miért van az, hogy fizeted a hiteled éveken át, és ha megkérdezed a bankot, hogy mennyi a tőketartozásod, kiderül, hogy alig csökkent?
Az annuitásos törlesztésnél a törlesztőrészleten belül a törlesztett tőke és kamat aránya folyamatosan változik. A futamidő elején magasabb a tőketartozás összege (mivel még nem, vagy csak alig törlesztettél), aminek viszont a kamata is magas.
Ahhoz, hogy a törlesztőrészlet ne legyen túl magas, és egyenlő összegű maradhasson a kamatperiódus alatt, a magas kamatösszeg mellé csak kisebb tőkerész törlesztése fér bele havonta.
A futamidő elején tehát sok kamatot fizetsz és kevés tőkét törlesztesz. Ahogy azonban csökken a tőketartozás, úgy fokozatosan az arány megfordul, mivel egyre kevesebb kamatot kell fizetned rá. A kevesebb kamat mellé pedig egyre nagyobb tőkerészek törlesztése fér bele a törlesztőrészletbe.
Minél hosszabb a futamideje a hitelednek, annál több kamatot fizetsz a banknak. A hosszabb futamidő miatt a havi törlesztőrészletek alacsonyabbak, cserébe akár több millió forinttal többet fizetsz vissza a banknak.
Annuitás vs. lineáris törlesztés
Ezzel szemben, ha minden hónapban ugyanannyi tőkét törlesztenél a futamidő során, akkor a havi törlesztőrészleted a futamidő elején rendkívül magas lenne: összeadódna a kezdetben magas kamat és a minden hónapban azonos mértékű tőketörlesztés.
Később egyre csökkenne a törlesztőrészlet, ahogy a tartozásod fogy, mivel a csökkenő tőketartozásra számított kamat egyre kevesebb lenne. Ezt hívják egyenletes vagy lineáris tőketörlesztésnek.
Annuitás nyugdíj-megtakarításoknál
Az annuitás befektetéseknél, így nyugdíjmegtakarításoknál úgy működik, hogy az egyszeri befizetésből vagy folyamatos megtakarításból annuitásos jövedelmet biztosít idős korban.
Az annuitásos kifizetés révén nem egyszerre kapja meg addigi megtakarítását a nyugdíjas, hanem rendszeres, egyenlő összegű havi kifizetéssel egy adott időszakon keresztül.
A gyakorlatban kétféle kifizetés történhet:
- határozott idejű (pl. 10, 15, 20 évig),
- életjáradék formájában (határozatlan időre, amíg az ügyfél él).
Az életjáradék és annuitás különbségét az jelenti, hogy bár mindkettőnél rendszeres havi kifizetésre kerül sor, de kockázatviselést tekintve eltérnek.
Az annuitásos, határozott idejű kifizetésnél az ügyfél viseli annak kockázatát, ha tovább él, mint az előre meghatározott időtartam.
Ezzel szemben az életjáradék az ügyfél életének végéig jár, és a biztosítóé a kockázat, hogy az ügyfél tovább él, mint a statisztikai átlag. Ebben az esetben a tőkét meghaladóan fizet a biztosító. Az életjáradéknál a biztosító statisztikák alapján számolja a havi összeget.
Amivel ezeknél a nyugdíjcélú befektetéseknél számolni kell, hogy az infláció csökkentheti az annuitás értékét, azaz amikor sor kerül a kifizetésre, a havi összeg jóval kevesebbet fog érni, mint a megtakarítás elindításakor.
Az annuitás számítása
Az annuitás számítás képlete segítségével kiszámolható a havi törlesztőrészlet, például futamidő alatt végig fix kamat esetén:
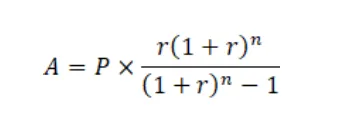
- A: a havi törlesztőrészlet
- P: a kezdőtőke, vagyis a felvett hitel összege
- r: a kamatláb periódusonként (azaz havonta a kamat)
- n: a periódusok száma (a futamidő hónapjainak száma)
Annuitásos lakáshitel példa
Nézzünk egy példát: ha 20 millió forint lakáshitelt veszel fel, 7,5%-os végig fix kamattal, 20 éves futamidőre, mekkora lesz a havi törlesztőrészlet?
Hitelösszeg: P=20 000 000 Ft
Kamat: r=7,5%/12=0,00625
Futamidő: n=20×12=240 hónap
A számokat a képletbe beírva ezt kapjuk:
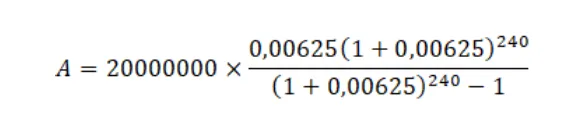
Ha ezt kiszámoljuk, akkor A≈161 119 (kerekítve), vagyis a havi törlesztőrészlet 161 119 Ft.
A futamidő alatt végig fix kamatú hitelek mellett persze különböző kamatperiódusú hitelekkel is találkozhatsz: 3 hónapos, 6 hónapos, 1 éves, 3 éves, 5 éves, 10 éves kamatperiódusúakkal. A bank ezeknél egy-egy kamatperiódus indulása előtt mindig újraszámolja a törlesztőrészletet.
Tehát, ha például a 20 éves futamidejű hiteled 5 éves kamatperiódusú, akkor négyszer fog változni annak kamata és törlesztőrészlete a futamidő alatt.
Nyugdíjcélú annuitás esetén
Nyugdíjcélú megtakarítás esetében ugyancsak ezt a képletet tudjuk használni a havi járadék kiszámításnál:
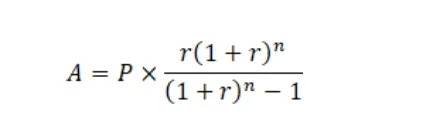
Ebben az esetben:
- P: az összegyűlt megtakarítás
- r: hozam/év
- n: a várható kifizetések száma (hónapok száma)
- A: a rendszeresen fizetendő járadék
Ha azt akarod kiszámolni, hogy mekkora összeget kell félretenni a nyugdíjba vonulásig, ha 20 éven keresztül havi 200 ezer forintos járadékot szeretnél kapni, akkor át kell rendezni a képletet így:
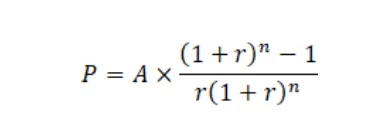
Valamint feltételezni kell egy hozamot, amit a befektetés és a piaci helyzet is befolyásol, de ha mondjuk 4%-kal számolunk, akkor így néz ki a képletünk:
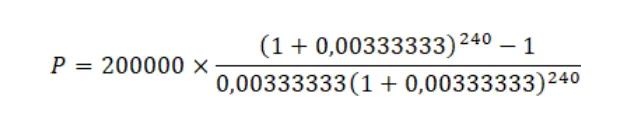
A szükséges megtakarítás nagysága itt nagyjából 33 millió forint lesz. (Ha magasabb a hozam, akkor milliókkal kisebb összeg szükséges.)
És mekkora havi összeget kell félretenni 30 éven át ahhoz, hogy ezt a 33 milliót összegyűjtsük, mondjuk megint egy feltételezett 4%-os hozammal számolva?
Az annuitás jövőérték képlete így néz ki:
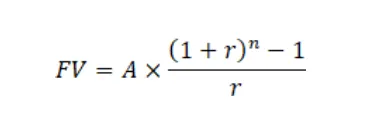
Itt:
- FV: future value vagyis jövőbeni érték, azaz 33 millió Ft
- A: havi befizetés összege (ezt akarjuk kiszámolni)
- n: futamidő (30 év, vagyis 360 hónap)
- r: a hozam (4%)
Ha a képletet átrendezzük A-ra, akkor így fog kinézni:
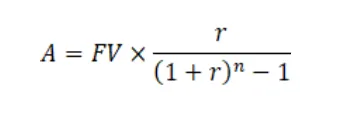
Ha beírjuk az értékeket, akkor pedig így:
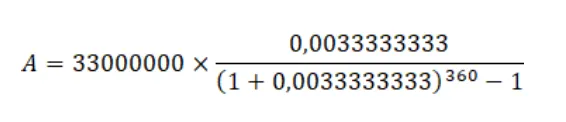
Ha ezt kiszámoljuk, akkor A≈47 500 Ft lesz, azaz ennyit kell félretenni havonta 30 évig, hogy nyugdíjasként 20 évig havi 200 ezer forintot kapjunk, mindezt 4%-os hozam mellett, ami nyilván lehet nagyobb is, és akkor sokkal jobb helyzetben leszünk.
És itt persze megint számolni kell az inflációval, ami miatt a 33 millió forint megtakarítás, illetve a 200 ezer forint vásárlóereje lényegesen kisebb lesz 30, illetve 40-50 év múlva.
Maradtak kérdéseid?
-
Miben különbözik az annuitásos és a lineáris törlesztés?
Az annuitásos törlesztés esetén kamatperióduson belül minden hónapban azonos a törlesztőrészlet, míg lineáris törlesztés esetén folyamatosan változik a tőkerész csökkenésével párhuzamosan.
-
Milyen pénzügyi termékeknél alkalmazzák az annuitást?
Az annuitás megjelenik hiteleknél, befektetéseknél, nyugdíjbiztosításoknál.
-
Hogyan számítható ki az annuitásos törlesztőrészlet?
Az annuitás számításnak létezik képlete, melynek segítségével kiszámolható a havi törlesztőrészlet, ugyanakkor ezt a számítást a webes kalkulátorok lényegesen egyszerűbbé teszik.
-
Milyen előnyei vannak a nyugdíjcélú annuitásnak?
A nyugdíjcélú annuitás fő előnye, hogy meghatározott, minden hónapban azonos összegű havi járadékot kap az ügyfél nyugdíjba vonulása után meghatározott ideig.
A fenti cikkben szereplő megállapításokat a Biztos Döntés Kft. a releváns tények és körülmények lehető leggondosabb szakmai értékelése alapján igyekezett megfogalmazni. Ebből adódóan a fenti írás nem tényközlés, hanem a Biztos Döntés Kft. – megfontolt és felvállalt – szakmai véleményét jeleníti meg.




